|
Maximum Detour and Spanning Ratio |
|||||||||
|
Maximum Detour and Spanning Ratio |
Introduction
Detour
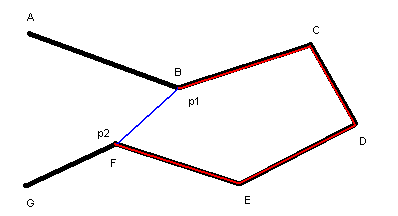
The detour from a point p1 to a point p2 of a plane graph G is defined as the ratio of distance saved by cutting across the graph. For example, in the following path, we can compute the detour from a point located on vertex B to a point on vertex F:
Figure 1: Detour from point p1 on B to point p2 on F on a path ABCDEFG
The detour D(G, p1, p2) of this graph would be computed as follows:
D(G, p1, p2) = ||(p1, p2)||G
||(p1, p2)||
Maximum Detour and Spanning Ratio
The maximum detour of a graph D(G) is the detour of a distinct pair of points (p1, p2) located on any edge or vertex of the graph such that the value D(G, p1, p2) is the greatest. Symbolically,
D(G) = maxp1, p2 {D(G, p1, p2) : ( p1, p2 Є UeЄEe ) ∩ ( p1 ≠ p2 )}
The spanning ratio of a graph S(G) is the detour of a distinct pair of vertices (v1, v2) of the graph such that the value D(G, v1, v2) is maximized.
S(G) = maxv1, v2 {D(G, v1, v2) : ( v1, v2 Є V ) ∩ ( v1 ≠ v2 )}
We will demonstrate an algorithm, by Langerman, Morin and Soss [1], that computes these values exactly on a polygonal path with expected running time O(n log n). The paper in question also talks about how to solve efficiently the same problem applied to simple cycles and trees.
|
Previous |
Next |
|
|
|
| Definition |
|
Maximum Detour and Spanning Ratio |
|||||||||
This page was created as a learning tool in Computational Geometry. It should not be reproduced without the consent of its author.
Félix-Olivier Duguay
School of Computer Science, McGill University
3480 University St., Suite 124
Montréal, Québec, CANADA, H3A 2A7
Last modified 2002-12-05