Searching

Back to the original problem: now that we have a trapezoidal decomposition of S, how can we determine which trapezoid our query point q lies in?

We would like to make some kind of decision tree, composed of simple queries that we can use to narrow down the location of q (like a binary search). Each node of this tree represents an individual query: it has out-degree 2, corresponding to a yes-no question. The leaves should point to individual trapezoids - once we hit one of these leaves we have determined which trapezoid q is in, and thus which face q is in.

For each leaf, we store a pointer to the face that trapezoid lies in

We will use two kinds of queries:

- point query: does q lie to the left or the right of a given point?
- segment query: does q lie above or below a given line segment?

Although we could accomplish what we need with just the second kind of query, the combination of these two queries works very will with our trapezoidal map.

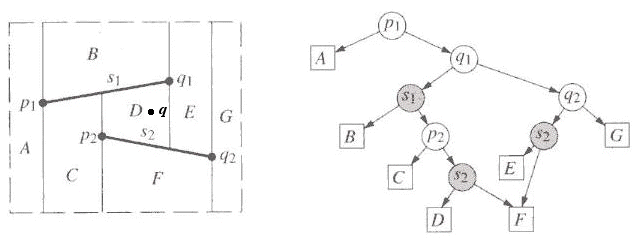
A possible decision tree D for the trapezoidal map of T is shown below:

Result of performing a search against the point q is shown below. The colors show where the point can still lie after we have tested against current node.

We start our query at the root of the search structure against point p₁.

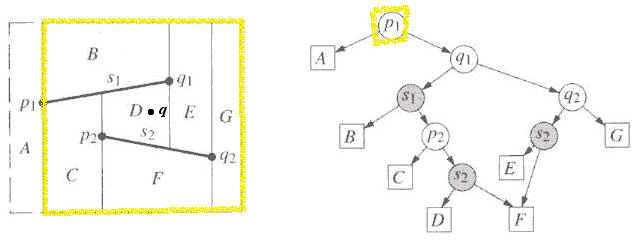
It lies to the right, so the query is against the point q₁:

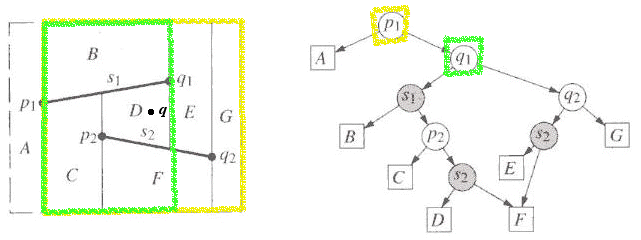
It lies to the left, so we move on to query against the segment s₁:

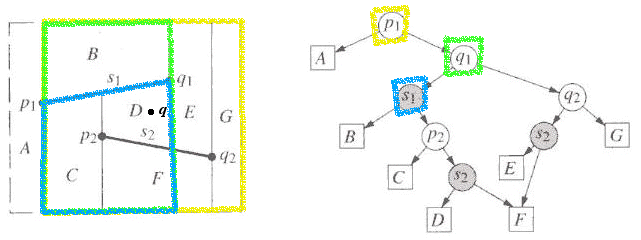
It lies below, so query is now against the point p₂:

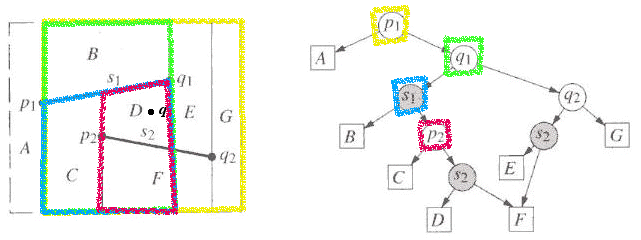
It lies to the right, so query against segment s₂:

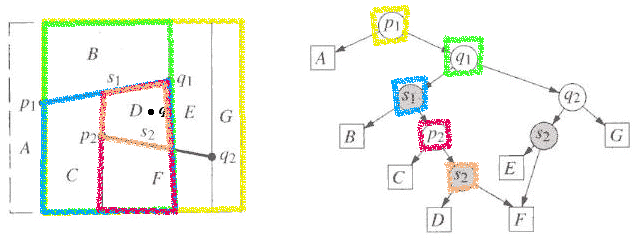
It lies above, and the next node is a leaf so we now know that q lies in trapezoid D.

At first it may seem like that D is a tree but it is not, actually it is a directed graph. So it is possible to found the same trapezoid by traveling totally different route, look at the picture above.