Introduction

The Problem and the motivation

The problem is next: Imagine that you are flying with your airplane and you have a map of the world in your computer and your GPS tells your position (latitude/longitude). You want to keep track of the all areas that you cross. Of course you are lazy and you do not want to do this by hand, so you want to make your computer to do this for you. But how do you do this? Well your map is nothing more than a planar subdivision and the reading from the GPS is your position. So we have a set of non-intersecting line segments in a plane and a point q inside one of those areas. The airplane is very fast so also your search algorithm has to be fast.

Some history of the point location problem

As you might already guessed that point location problem has indeed a long history in computational geometry. Preparata and Shamon presented early results already in 1985. Four basically different approaches lead to optimal O(log n) search time and O(n) storage solutions. Those four were the chain method by Edelsbrunner et al. [1], which is based on segment trees and fractional cascading, the triangulation refinement method by Kirkpatric [2], the use of persistency by Sarnak and Tarjan [3] and Cole [4], and the randomized incremental method by Mulmuley [5].

First Idea

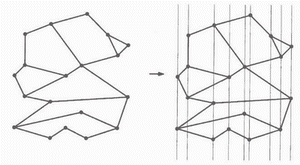
Naive algorithm would draw vertical lines through all vertices of the subdivision as show in figure 1.1. We store the x-coordinates of the vertices in sorted order in an array. Each slab contains no vertices, so the regions within are nicely ordered from top to bottom.

We take advantage of this fact by storing the segments that each slab intersects in an array

Algorithm for Point Location

- Do a binary search by x-coordinate of q against the x-coordinates of the vertices of S to determine which slab q lies in
- Do a binary search of q against the segments intersecting this slab
- The label of the edge just below q tells us which face the trapezoid, and thus q, lies in

Figure 1.1 Partition into slabs

Analysis

Total running time is O(log n):

O(log n) - binary search against O(n) vertices of S
O(log n) - binary search against up to n segments intersecting the slab

What about storage space? For each slab, we need to keep an array long enough to hold all of the segments intersecting the slab. Storage space required can be as bad as O(n²) figure 1.2.

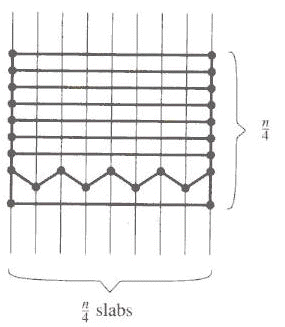
Figure 1.2. Space required can be as bad as O(n²)

Although it may not be quadratic in practice, the textbook [6] suggests typical storage required would be O(n^3/2).

Our algorithm seems good because it has good query time but it can take lots of space. So to improve our algorithm we need to improve our data structure. The improved data structure is called the Trapezoidal map.