An Incremental Randomized Algorithm

We are going to use an incremental algorithm. It will take one segment at time and after every addition it will update the trapezoidal map and the search structure. This means that after every loop we have valid trapezoidal map and search structure for it.

Algorithm TrapezoidalMap(S)

1. Determine a bounding box R that contains all of the segments of S
2. Initialize T, the trapezoidal map structure and D, the search structure:

    T is just the single trapezoid corresponding to the whole box R
    D has only one node, corresponding to that trapezoid
3. Compute a random permutation s₁, s₂, ..., s_n of the segments of S
4. for i ß 1 to n

    do Find the set of trapezoids in T properly intersected by s_i
5.             Remove them from T and replace them by the new trapezoids that appear because of the insertion of s_i
6.          Remove the leaves of D for the old trapezoids and create leaves for the new ones. Link them to the existing inner nodes by adding some new inner nodes, as explained later

Key features of the algorithm:

-Incremental: Every time we insert a segment, we have a complete trapezoidal map and a complete data structure for the segments inserted before.
-It uses randomness, so there are no bad inputs.

Finding Intersected Trapezoids

How to add a new segment s_i?

Let D₀, D₁, ..., D_k be the trapezoids intersected by s_i, ordered from left to right.

D₀ is the trapezoid containing the left endpoint p of s_i. To find it, perform a query on D (the data structure corresponding to the segments inserted so far) with p. We have to be careful if p was already present as an endpoint (assume the new point is slightly to the right).

D_j+1 must be a right neighbor of D_j, and it is easy to determine which one: If rightp(D_j) lies above s_i, then D_j+1 is the lower right neighbor of D_j, otherwise it is its upper right neighbor, Figure.

Algorithm FollowSegment(T, S, s_i)

    1. Let p and q be the left and right endpoint of s_i.
    2. Search with p and q in the search structure D to find D₀.
    3. j ß0;
    4.      while q lies to the right of rightp(D_j)
    5.                  do if rightp(D_j) lies above s_i
    6.                      then Let D_j+1 be the lower right neighbor of D_j lies.
    7.                  else Let D_j+1 be the upper right neighbor of D_j lies.
    8.                  j ßj + 1
    9.      return D₀, D₁, ..., D_j

Incrementing T and D - Simple Case

How are T and D updated?

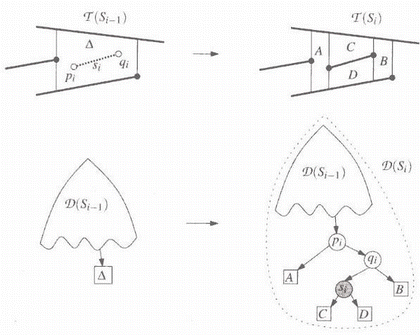
Simple case: s_i is completely contained in one trapezoid D (Figure 3.1)

 - In T, D is replaced by 4 trapezoids and update also their neighbors records.
 - In D, the leaf corresponding to D is replaced by a small tree with 2 point nodes, 1 segment node, and 4 leaves, note that if one or both endpoints equal to leftp(D) or rightp(D) then there would be only two or three new trapezoids.

Notify that all the needed information is available in constant time from the segment s_i and from the information stored in D.

Figure 1.1 The new segment lies completely in trapezoid D.

Incrementing T and D - General Case

General case: s_i intersects D₀, D₁, ..., D_k

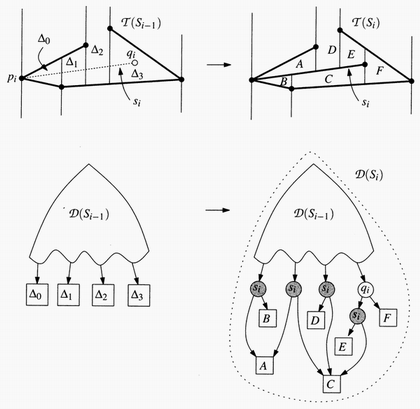
Figure 1.2 Segment s_i intersects four trapezoids.

To update T:

- Draw vertical extensions through the endpoints of s_i that were not present, partitioning D₀ and D_k  
- Shorten the vertical extensions that now abut on s_i, merging the appropriate trapezoids. This leads to merging trapezoids along the segment s_i, (Figure 1.2). Use the information stored to D₀, D₁,...,D_k to determine all the needed data. This step can be done in linear time.

To update D:

Remove the leaves for D₀, D₁,...,D_k

- Create leaves for the new trapezoids
- If D₀ has the left endpoint p of s_i in its interior, replace the leaf for D₀ with a point node for p and a segment node for s_i (similarly with D_k)
- Replace the leaves of the other trapezoids with single segment nodes for s_i
- Make the outgoing edges of the inner nodes point to the correct leaves. Notify that many inner nodes could be pointing to the same leaf.