Expected Performance
As I mentioned earlier, the correctness of the algorithm follows directly from the loop invariant, so the only thing we what needs to be do is the performance analysis.
For some insertion orders, the resulting search structure may have quadratic size and linear search time. For other permutations it is much better. We took a random insertion sequence, so we are interested in the expected performance. The expected time is the average of the running time, taken over all n! permutations
Theorem.
- This algorithm computes T and D from a set S n line segments in general position in O(n log n) expected time
- The expected size of D is O(n)
- For any query point q the expected query time is O(log n)
Proof:
Expected Query Time is O(log n)
Fix a query point q, and
consider the path in D traversed by the query.
Define
Si = {s1, s2,
..., si}
Xi = number of nodes added to the search path for q
during iteration i
Pi = probability that some node on the search path of q
is created in iteration i
Dq(Si) = trapezoid containing q in T(Si)
From
our construction, Xi £ 3; thus E[Xi] £
3Pi
Pi = Pr[Dq(Si)
Ļ Dq (Si-1)]
Backwards
analysis:
How
many segments in Si affect Dq(Si) when
they are removed? At most 4. Since they have been chosen in random order, each
one has probability1/i of being si. So, Pi
£ 4/i.
![]()
Let Hn = 1 + 1/2 + 1/3 + ... + 1/n, and recall that Hn = Θ(log n), in particular for n > 1 we have loge n < Hn < 1 + loge n.
Proof:
Expected Storage Size is O(n)
The
total number of nodes is bounded by
![]()
where ki = number of new trapezoids created in iteration i.
|
Define d(D,s) = |
{ |
1 if D disappears
from T(Si) when s is
removed from Si |
|
0 otherwise |
![]()
![]()
So, the expected amount of storage is O(n).
Proof:
Expected Construction Time is O(n log n)
The
time to insert segment si is O(ki) plus the
time needed to locate the left endpoint of si in T(Si-1).
So, the expected running time of the algorithm is
![]()
Using tail estimate one can prove that let S be set non-crossing line segments and let l be a parameter with l > 0. Then the probability that the maximum length of a search path in the structure for S computed by algorithm TrapezoidalMap is more than 3lln(n+1) nodes is at most 2/(n+1)lln1.25-3.[6]
Surprise surprise this is not end of the story, Raimund Seidel [8] has showed that if S is given as a simple polygonal chain the expected running time of his algorithm is O(n log* n) and more generally if S is presented as a plane graph with k connected components, then the expected running time of his algorithm is O(n log* n + k log n). His algorithm also takes O(n) space for the search structure and query can be done also in O(log n) time.
Removing Our
Assumptions
We can get rid of the assumption
that no two distinct endpoints have the same x-coordinate.
Observation: The vertical direction that we chose was
immaterial.
1st Idea: Rotate the axis system
slightly
This
can lead to numerical difficulties, and requires an extra pass through the
data.
Improved
Idea: Apply affine mapping (shear transformation)
F(x, y)=(x + ey, y) for small enough e.
This
mapping preserves straight lines, so any "insidedness" holds just as
true as it did before we applied the shear.
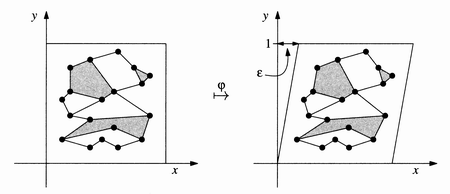
Symbolic
Transformation
In practice, we donít have to
apply any transformation. We get the result using lexicographic order (compare
first by x-coordinate, then by y-coordinate):
The only two operations used in the
algorithm were:
Decide
if q lies to the left of p, to the right, or on the vertical line
through p.
Decide whether q lies above, below, or on the segment with endpoints p1
and p2.
Both
can be done without actually computing F.
Moreover, it is equivalent to the
limit of these shears as e approaches zero (from the positive
side).
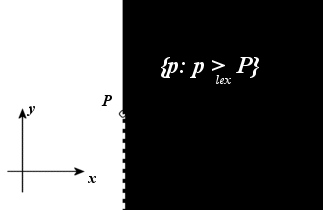
This
modification also makes the other initial assumption unnecessary: A query point
never lies on the vertical line of a point node, or on the segment of a segment
node.
Conclusion: Our algorithm TrapezoidalMap computes the trapezoidal map T(S) of a set S of n non-crossing line segments and a search structure D for T(S) in O(n log n) expected time, it takes O(n) space to build the search structure and for any query point q the expected query time is O(log n).