The Data Structure
1. The Trapezoidal Map
Although the previous algorithm was inefficient in terms of space usage, it had some very nice properties:
- the entire map was broken into
trapezoidal sections (and triangles, which we treat as degenerate trapezoids)
- each trapezoid has exactly 2 non-vertical boundaries
- no trapezoid contains a vertex (all are at corners)
- each trapezoid belongs to exactly one face
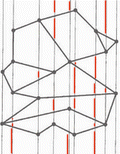
We want to preserve these properties but reduce the complexity of our structure. We can remove many edges without destroying these properties shown in figure 1.1

Figure 1.1 Destroying edges
Removing all unnecessary edges and adding axis-parallel rectangle R that contains the whole scene (to get rid of the unbounded trapezoid-like faces that occur at the boundary of the scene) gives us the trapezoidal map figure 1.2 (also trapezoidal/vertical decomposition) T(S) of S.
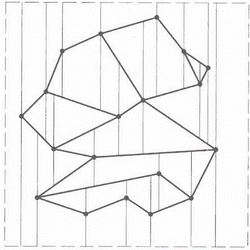
Figure 1.2 Trapezoidal map
Formally, the trapezoidal map of S is obtained from S by taking a planar subdivision, and drawing two vertical extensions from each vertex: an upper vertical extension, and a lower vertical extension.
The extensions go vertically up/down from the vertices of S and stop when they hit an edge or the bounding box R.
The trapezoidal map is guaranteed to be not much more complex than the original map; if we started with n line segments than we can end up with no more than 3n+1 trapezoids.
Proof. A bound in the number of trapezoids follows from Euler's formula and the bound in the number of vertices. Direct proof uses the point leftp(Δ). This point is the left end point of one of the n segments, or it is the lower left corner of R. By looking at the five cases for the left side of trapezoid, we find that the lower left corner of R plays this role for exactly one trapezoid, a right endpoint of a segment can play this role for at most one trapezoid, and a left endpoint of a segment can be the leftp(Δ) of at most two different trapezoids. It follows that the total number of trapezoids is at most 3n + 1.
2. Assumptions / Simplifications
Want to deal with a bounded region instead of the entire plane:
- look at all vertices and
determine xmin/max, ymin/max
- put a bounding rectangle around all of the points
- when queried, if query lies outside the box then q lies in the
unbounded face and we are done; here forth we will assume q lies inside
the bounding box
Since we are dealing with vertical lines, it will be easier to assume all x-coordinates of all vertices and of the query point are distinct. We generalize from a planar subdivision to an arbitrary collection of non-crossing segments.
3. Navigating the Map
Lemma: Each face in a trapezoidal map of a set S of line segments in general position has one or two vertical sides and exactly two non-vertical sides
For any trapezoid D, define
top(D) - the line segment (either of S
or the bounding box) which bounds D
from above
bottom(D) - the line segment
(either of S or the bounding box) which bounds D from below
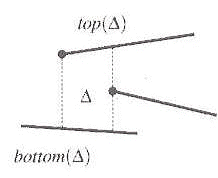
Figure 3.1 Trapezoid D
We can also define the left and right endpoints of D, leftp(D) and rightp(D), although there are five different cases to consider (we consider only the leftp(D), the other five cases for the right side of a trapezoid D are symmetrical) figure 3.2.
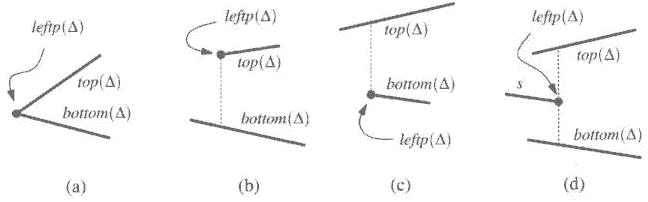
Figure 3.2 Four of the five cases for the left edge of trapezoid D
a) the left side is a point at
which top and bottom meet
b, c) the left side is formed by a single vertical extension of a point
d) the left side is formed by both vertical extensions of a point
e) the left side is the edge of the bounding box, which occurs only for a
single trapezoid
For every trapezoid D, top(D), bottom(D), leftp(D) and rightp(D) define the edges and vertices of that trapezoid. So we will store trapezoids as a 4-tuple of points/edges.
We will call two trapezoids adjacent if they share a vertical boundary. In figure 3.3 for example, trapezoid D is adjacent to D1, D2 and D3, but not to D4 and D5, Figure 3.3(i). Because the set of line segments is in general position, a trapezoid has at most four adjacent trapezoids. If the set is not in general position there could be an arbitrary number adjacent trapezoids, this case is shown in Figure 3.3(ii).
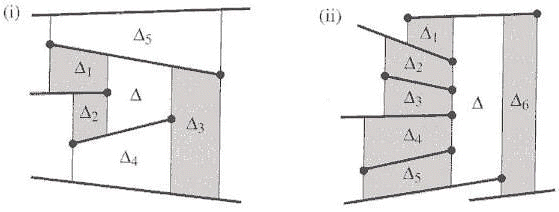
Figure 3.3 Trapezoids adjacent to D are shaded
However, our assumption that no two points share the same x-coordinate makes this impossible. How many neighbors can a given triangle D have on the left side?

- it will have no neighbors if top
and bottom meet at leftp or D
is on the edge of the bounding box
- it will have one neighbor if leftp is an endpoint of top or bottom
- it will have two neighbors if leftp splits the left side in half
So on the left and right sides together it may have up to four neighbors; we
will call these the upper left, lower left, upper right, lower
right neighbors of D.
4. Records
Because the special shape of the trapezoid we don't have to use for example doubly-connected edge lists to present the trapezoidal map so we only keep records of all line segments and end points of S, this because they are the top(D), bottom(D), leftp(D) and rightp(D). Then we also need records for the trapezoids of T(S), the record for trapezoid D stores pointers to top(D), bottom(D), leftp(D) and rightp(D) and pointers to its at most four neighbors. This information is enough to determine the geometry of D in constant time.