
So lets try to answer the first question. How many triangulations does a convex polygon have? A triangle has just one,
a quadrilateral has two and a pentagon has 5, a hexagon has 14,...............! So what about 'N' ?
The way to do it is to imagine a recursive construction of the triangulation of a convex polygon.
Lets take the edge V1 to Vn as a base.
Choose the apex of the triangle to which this belongs, called Vj.
So now we are left with two polygons on either side of
this diagonal
which can triangulated in a
similar manner, by choosing their respective base segments. This gives rise to the fact that there is recurrence relation
behind these triangulations.
The number T(n) of triangulations of an n-gon is given as:
T(2) * T(n-1) + T3 * T(n-2) + T4 * T(n-3) + ............+ T(n-1) * T(2), where T(2) and T(3) are both unity, trivially.
This recurrence relation gives us the (N-2)th "CATALAN NUMBER". The
Catalan number is given as:
Catalan (N)
= (1/N) * Choose (2N,N)
The (N-2)th Catalan Number, which is the number of triangulations of an N-gon
is:
Catalan (N-2) = (1/(N-1)) * Choose (2N-4,N-2)
Putting different values of N in this formula, we get the value of 1
for a triangle, 2 for a quadrilateral, 5 for a pentagon, 14 for a hexagon,
42 for a heptagon, 132 for an octagon and so on. Have a look below,
and then perhaps try imagining what it might be for N = 20!!
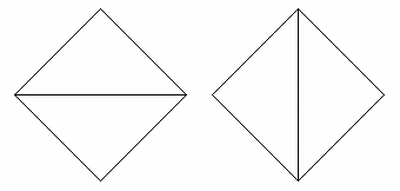
4 vertices and 2 triangs.

5 vertices and 5 triangs.
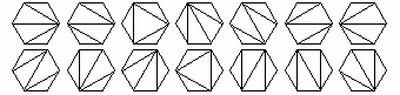
6 vertices and 14 triangs.
7 vertices and 42 triangs.
So I guess, we have answered our first question. (There are many interesting sites on Catalan Numbers, one of which is listed right
below.) Now for the second and more difficult one. To answer this, we
are basically going to study the Hierarchy of Triangulations, as proposed by Hurtardo and Noy. And then look at a Randomized method for
the same purpose.
But before all that a few small things. If you observe carefully, you will
realize that the adjacent triangles in a
triangulation form a quadrilateral. The common edge of the two triangles is a diagonal of the quadrilateral.
Given the current triangulation, another one can be created by merely FLIPPING this diagonal, i.e. removing it from the
quadrilateral
and adding in the other one. If T1 was the former triangulation and T2 is the new one, we say that T1 and T2 are adjacent
or we write T1~T2. This is obviously a symmetric property. But T2 may not be the only one that can be created from T1. There are
several diagonals in a triangulation, and each flip thus yields a completely different triangulation, "obtained" from the original one.
Moreover given a convex polygon (or a simple polygon or a point set for that matter), any of its
triangulations can be transformed into any other of its triangulations by a finite number of flips.
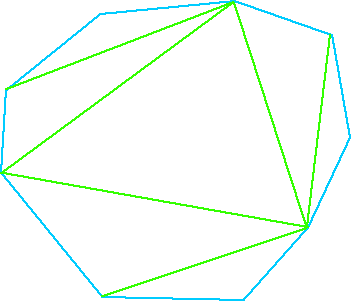
Look at this figure here below, for instance. Its shows the "circular" sequence of flips for a pentagon:
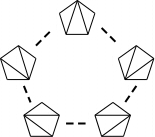
A circular sequence of flips
The interesting thing here is that triangulations can be organized in a hierarchy as nodes of a certain tree of infinite size. This
hierarchy is helpful in proving a lot of interesting properties pertaining to the "Graph of Triangulations", i.e. a Graph with a
triangulation for each node, and an edge between two nodes if they represent triangulations differing by the flip of a single diagonal.
This part however is beyond the scope of our current discussion. Refer [1] for further details.
Let T(n) be the complete set of triangulations of an n-gon. Every triangulation t belonging to T(n) has a "father"
in T(n-1) and one or more "sons" in the triangulation T(n+1). In other words, given a T(n), we can actually
generate the triangulations of the (n+1)-gon from every such t. The number of sons of t is dependent on the
outdegree of the
vertex Vn.
Thus, the triangulation Si which is a son of t, given the edge E(i,n) in t, will consist of edges that are the union of the following:
What we are basically doing is opening the parent polygon and adding in the (n+1)th vertex. We keep all edges of the parent that did not involve Vn as they were. Next we remove all edges of the form E(p,n) from the parent and add in E(p,n+1) instead. Thereafter we add in all edges E(p,n) of the parent, where p was a vertex numbered higher than 'i' (remember we are constructing the 'i'th son). And lastly we close the polygon with the edge E(n,n+1). Have a look at the following figure:
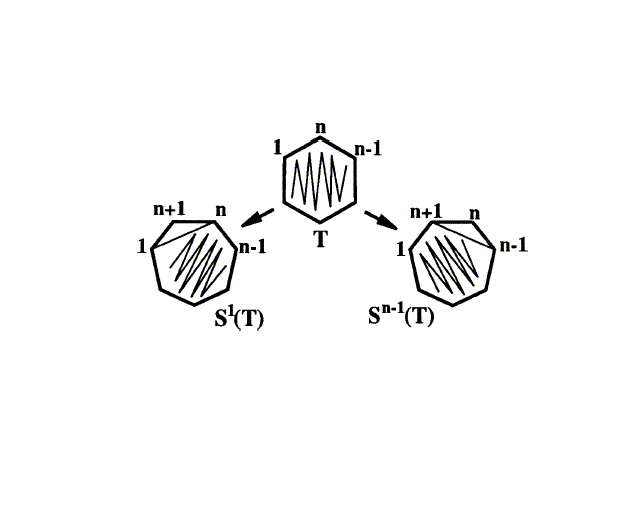
Sons of the same father.
So if there are 'd' vertices connected to Vn in a parent, it will clearly have exactly 'd' sons. If t1 and t2 have the same parent, we shall call t1 and t2 as siblings. Again, by induction we easily have an infinitely sized "tree" which goes on expanding like "wild fire". Have a look at the figure below.
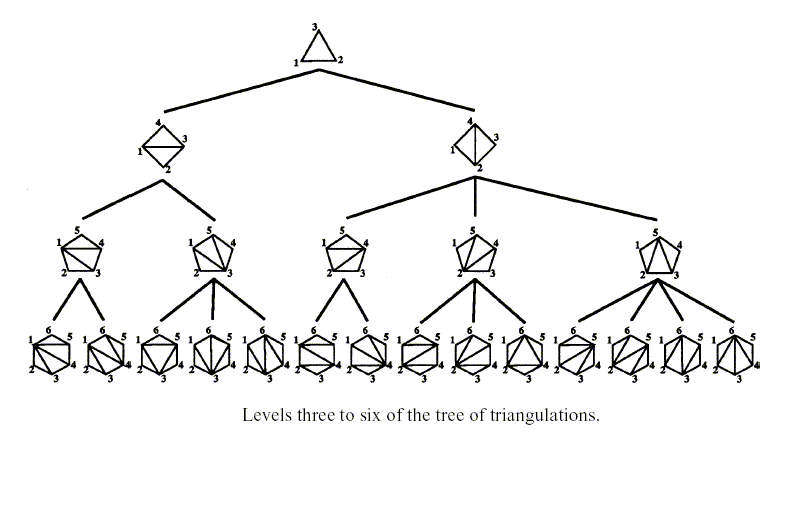
The Hierarchy
This method is a very inviting way to generate all triangulations, despite its very high time complexity, tending to be exponential. Indeed, we even need the triangulations of the (n-1)th polygon ready. And then we generate 'd' sons for each of those, where 'd' is the degree of Vn of each triangulation. The process of union of those 4 sets would be an O (n) operation. However the hierarchy is nevertheless important because of its inherent simplicity and also owing to the fact that it has a number of really exciting properties which we shall state below. These properties can be viewed by going through the applets 1 and 2 carefully.
Before stating the algorithm, we need to go deep into a very interesting correspondence between triangulations and a
certain kind of lattice paths that we shall describe presently. (We already know that the dual graph of a triangulation of a convex polygon is always a tree, having n-2 internal
nodes. The degree of any internal node therein is at most 3. Due to this correspondence, the problem of enumerating the triangulations of a convex n-sided polygon, also bears analogy with the problem of enumerating all possible binary trees with n-2 nodes. But thats a digression here). Given a triangulation t in T(n),
we construct a path P(t), which starts at the point (1,0) and ends at
(n-2,n-3), making either upward or rightwards movements on its way. This
is nothing but a lattice path bounded on three sides by the X axis, by the
line y = x and by the line x = n-2. Suppose the first vertex i.e. V0 has
the outdegree d0. (By outdegree we here mean the number of
diagonals
starting from v1 and ending in a vertex with a higher number.) Then our path shall move d0 steps to the right. For all the other vertices Vm in clockwise order, if dm is the degree and dm > 0, then our path moves up to the line y = m and then dm steps to the right.
A triangulation is uniquely characterized by the set of outdegrees of its
vertices, and hence such a path always gives us a unique triangulation,
giving rise to the bijection. To have an example of this claim, look
at the diagram of the 5 triangulations of the pentagon.
Label the vertices from 1 to 5 in clockwise order, and write down the
outdegrees of all those vertices for each triangulation. You will clearly
notice that each triangulation has a unique set of outdegrees!
Note that this
path never crosses the
diagonal line y = x passing through the origin.Notice that the width of
the step at the line y = i, is equal to the outdegree of the vertex Vi.
(BTW - why are we starting from (1,0)? That's because, we want the path to
remain bounded by the line y = x. If we start from (0,0)), we shall have to modify this bound). Have a look at the following figure:
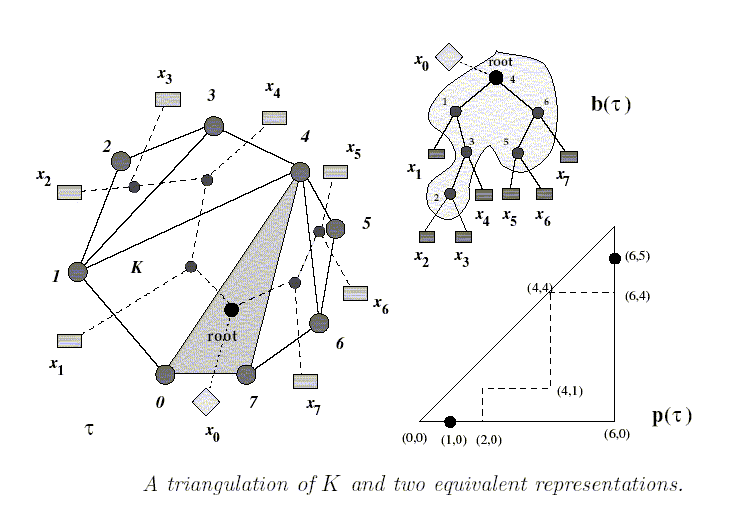
A triangulated Octagon, the corresponding tree and lattice path
The basic idea therefore is to generate the lattice path in some way. From the widths of the steps of the lattice path, we obtain the outdegrees of all vertices of the triangulated polygon. By a "greedy" kind of method, we can quickly infer the actual triangulation. All in O (n) time! So the question is how do we generate the path! And not just that, how do we generate all the paths so that we ultimately are able to generate ALL triangulations.
We make use of the Ballot Theorem , which says that the number of paths starting from (0,0) and making i steps to the right, j <= i steps upwards
and obeying the constraint that the path doesnt cross the line y = x, is given by
N(i,j) = (Choose (i + 1 + j, j)) * ( i + 1 - j) / (i + 1 + j)
Hence a path starting from (1,0) and ending at (n-2,n-2) preserving the required constraints is given by
N = (Choose (2n - 5 - k, n-2)) * (k+1) / (2n - 5 - k)
Let (Xm,Ym) be the point on the path after m steps of size 1, either up or right (m < 2n-4) starting from (1,0). There can be Catalan(n-2) paths, of which Catalan(n-3) pass through (1,1).
Let us deduce the probability that a path moves right or upwards. Suppose (Xm,Ym) = (i,j). From (i,j) to (n-2,n-2), there are totally N(i,j) paths given by
p = N(i+1,j) / N (i,j) = ((i + 2 - j) / (i + 1 - j)) * ((n - 2 - i)/(2n - 4 - i - j))
Now consider a sequence of random numbers between 0 and 1. Let the sequence be denoted as U1,U2,U3,....2n-4 times. At each step, we generate a random number. if the random number is less or equal to p, we decide to move right. Hence the next point after (Xm,Ym) is (Xm+1,Ym). Otherwise, we decide to move upwards and the next point is (Xm,Ym+1).
Next we give the algorithm to generate the random path.
Note that the algorithm proceeds with correct probability either right or up, and will never violate the constraints we had set. Moreover, it is an O(n) algorithm. The paper referred to here, also discusses a method to generate triangulations with exactly 'k' ears. Refer to the research paper for further details
The last part is about how we could infer the triangulation from the path. Look at the figure showing the triangulated octagon and its corresponding lattice path. We know the widths of all the lattice steps. Therefore, we also know the out-degrees of all the vertices of the triangulated polygon that we shall be constructing. Our job now is to infer the correct diagonals. The out-degree of V7 of the octagon (vertices from 0 to 8) is always obviously 0. So must be the out-degree of V6. In this case, the out-degree of V5 is 0, but that of V4 is given to be 2. There can be no diagonal connecting V4 and V5 as they are adjacent vertices, so we must have the diagionals V4-V6 and V4-V7. Proceeding ahead (or rather backwards, i.e. towards V0), V3 has outdegree 0, so does V2. But V1 has outdegree of 2. While inferring the diagonals of V1, we must check out for the nearest non-adjacent vertices that are greater than 1, and that do not cross the previously included vertices. Thus V2 being adjacent to V1, is ruled out, but V1-V3 can be included as it does not cross any previously included diagonal. V1-V4 is similarly acceptable. Thus we are left with only V0, which has outdegree 1. To infer the diagonal from V0, we see that V1 is ruled out. V2, V3 are ruled out as that would cross the diagonals from V1. That leaves us with V4, and indeed V0-V4 does not cross any other diagonal. This is clearly a naive implementation and is O (n*n) in time complexity. O (n) algorithms to convert a path into the triangulation do exist.
Applet to Enumerate All Triangulations at One
Go!
Note - for N >= 8, the process may be a little slow. Please be patient! Enter the desired value of N inside the edit box.
For convenience sake, we have restricted that value to 15.
Applet to Traverse the Tree by the
Selected Branch
The applet first display a triangle and its two children. You have to choose ONE of them by clicking INSIDE that particular polygon.
That causes generation of the children of that polygon and so on, till you have reached the value of N you entered in the edit box!