Let me remind you about the problem we are trying to solve. Given a set S of n line segments in the plane, compute all stabbing lines, or the lines which intersect all segments. In this section we'll present an algorithm for solving this problem, by using the characterization we found in the geometric preliminaries section. 

Determining stabbing region:

Given a set S of line segments, here is the algorithm which finds the stabbing region of the set. The algorithm is recursive and uses the divide-and-conquer technique.

• If |S| = 1 (there is only one line segment in S) ==> the stabbing region is the double wedge of this segment.
• If |S| > 1 == > divide S into two equal size subsets, and compute the stabbing region of each subset recursively. The stabbing region of the whole set will be computed by intersecting the stabbing regions of the subsets.

Merge step details and the complexity analysis are given in the complexities section.

Example:

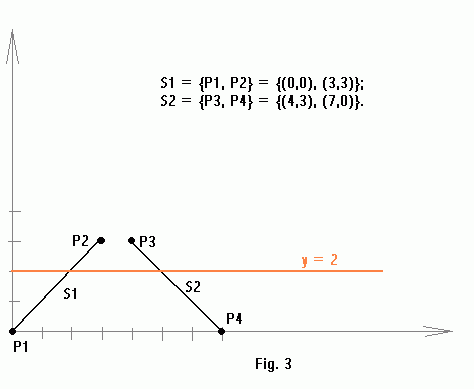
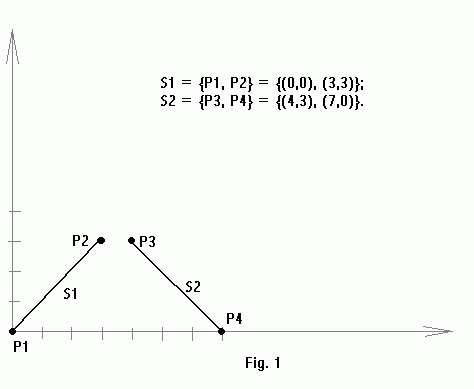
The line segments set in figure 1 consists of just two segments: S1 = {P1, P2} and S2 = {P3, P4} with the endpoints as indicated.

Let's look at the transform of these two line segments:

P1 = (0,0) ==> T(P1): y = 0;

P2 = (3,3) ==> T(P2): y = 3x + 3;

P3 = (4,3) ==> T(P3): y = 4x + 3;

P4 = (7,0) ==> T(P4): y = 7x.

Here is the double wedge corresponding to S1 segment:

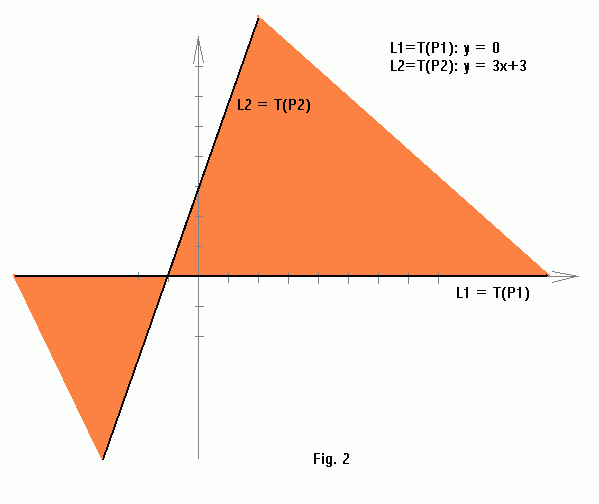
... and the double wedge corresponding to S2 line segment:

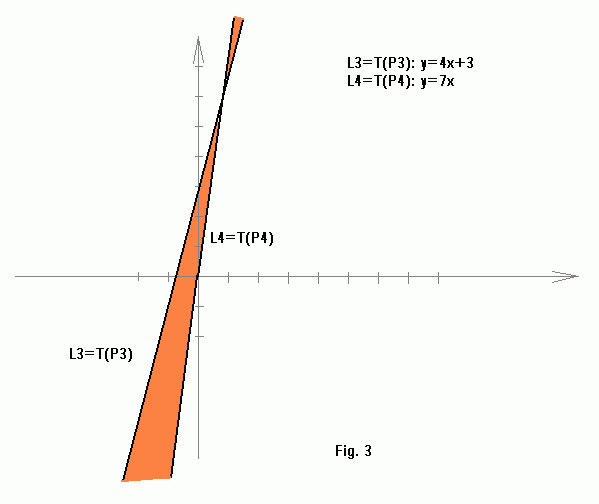
The stabbing region is the intersection of the double wedges corresponding to all the segments in the set:

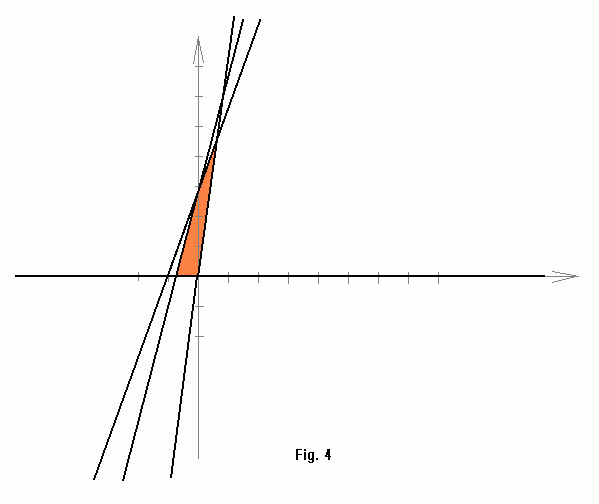
Finding stabbing lines:

Having obtained a stabbing region in the transformed plane, it's easy to find the stabbing lines by applying the reverse transform to the points inside the stabbing region. Every point in the stabbing region corresponds to one stabbing line.

The transform T' reverse to that introduced in the preliminaries section, is as follows:

P = (a,b) ==> T'(P): y = -ax + b;

L: y = kx + d ==> T'(L) = (k, d).

It's easy to verify that T(T'(P)) = P and T(T'(L)) = L.

In our example, any point inside the "orange" region in figure 4 determines a stabbing line.

Let's take, for example, a point P = (0,1). By applying the reverse transform we obtain a line y = 1. Indeed, this is a stabbing line for our segment set:

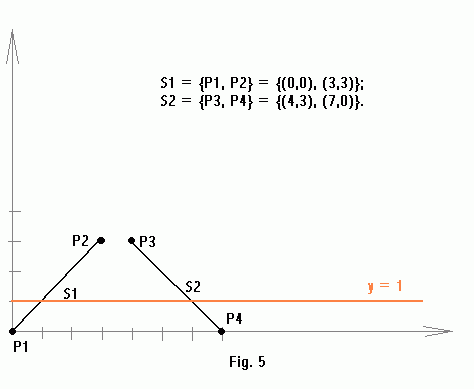
...And for a point P = (0,2) we obtain another stabbing line y = 2: