In general, the problems polygon models are used to represent are real-world applications, and thus it is appropriate to consider motions between configurations in 3 dimensions. To this end, we introduce the notion of motion in terms of pivots , where a polygonal chain of polygon P in R^d is reflected across a Hyperplane H which supports the convex hull of P and contains at least two vertices of P. Since we are considering the case where d=3 (i.e. R³ or 3D), the H is simply a halfplane which contains 2 points on the convex hull of P:





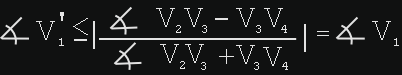
Theorem 2: Any planar convex polygon P can be reconfigured into any other planar convex polygon P' using pivots.

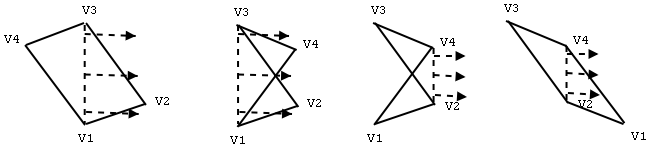
Proof: Locate a quadrangle V₁V₂ V₃ V ₄ where the vertices are labelled -, +, -, +, respectively, in P. Then, step through the following motions:

• Pivot on V₁V₃, rotating the entire subpolygon until V₂ is over V₁V₃.
• Pivot on V₂V₄ to bring the quadrangle into a planar configuration.
• Pivot on V₄V₁ to bring the subpolygon defined by those two vertices into the plane of the quadrangle.
• Pivot on the remaining three edges to bring each of their subpolygons into the plane of the quadrangle..
  

Lemma 4: Let V₁ V ₂V₃V₄ be a planar convex quadrangle. After two pivots, suppose the quadrangle is again planar, resulting in a quadrangle, V₁V₂ V₃V₄ . Then
< V₂V₁ V₄ will be at least the original value of the expression | <V₂ V ₁ V₃ - < V₄ V₁ V ₃ |.


Proof: If both pivots are on the diagonal V₂V ₄, then the angle at V ₁ has not changed, and so we must only consider the remaining cases, where the first (or both) pivot is on V₁V₃, and where the first pivot is on V ₂V₄ and the second is on V ₁ V ₃ .

    In the former case, the pivot must occur on a planar quadrangle, with the vertex of the quadrangle on the moving subpolygon--say it is V ₂-- tracing a circle around V₁V ₃ as it rotates, and thus the angle V₂V₁ V ₃ remains constant throughout the pivot. Since V ₄ remains fixed during the motion, the angle V₄ V ₁ V₃ also remains constant, and so the angle after the pivot must be at least the difference |< V ₂ V ₁V ₃ - < V ₄ V ₁ V ₃|.

    In the latter case, the two pivots must bring the quadrangle into a planar configuration, and the distance V₂V ₄ is increasing during the motion, so by the law of sines, < V₂V₁V₄ must also have increased, and so is greater than |<V₂V₁ V ₃ - < V₄V₁V₃ |.





This leads to the main theorem for this part:

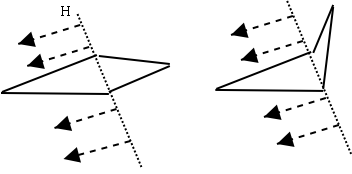
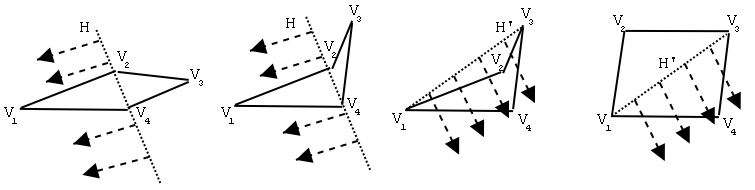
Theorem 3: There exist polygons which require arbitrarily many pivots to achieve a goal configuration.




Also, since for small angles <x, sin x ~ x, and so as <V₁ decreases, for every two pivots <V ₁ is only reduced to an angle <V₁^' where

    And so since <V₁approaches but does not attain zero (since we disallow the "flat" self-intersecting configuration that would result), a goal configuration with an arbitrarily low <V ₁can be chosen, so that an arbitrary number of pivots are needed to reconfigure the polygon. This is easily extended for arbitrary pivots by considering any arbitrary pivot as a pair of pivots on the same diagonal, where the first pivot brings the quadrangle into a planar non-intersecting position and the second produces the original pivot desired.

    So it is observed that there does indeed exist a motion between any two planar convex polygons using only pivots, but this motion is not bounded by the number of edges of the polygon-- it can be achieved with arbitrarily many pivots if we choose a configuration as in Theorem 3.

Back--Distance-Monotone Motions       Main      Next--Conclusion