Stereolithography Illustration

Geodesic Properties of Polygons

"More is in vain when less will serve." - Isaac Newton

In the manufacturing industry, there exist a variety of different processes for constructing an object. Such processes include injection-molding, casting, NC-machining, laser-sculpting, automated welding and rapid prototyping. Rapid prototyping subsumes a family of methods known as layered manufacturing processes such as stereolithography (also known as 3D-printing and depicted in the illustration above). Every manufacturing process imposes certain restrictions on the types of objects that can be constructed as well as the manner a given object may be built. For example, a sphere is difficult to build with stereolithography, but can be easily made using injection molding. A cube can be constructed easily using stereolithography only when placed on one of its faces.

Two fundamental questions arise concerning every type of manufacturing process:

The latter question gives rise to many different problems depending on what is meant by best. The geometry of the object, coupled with the restrictions imposed by the particular manufac turing process under consideration, play a vital role in determining the answer to these questions.

The importance of these questions is quite evident. For example, when designing an object to be built by a certain type of manufacturing process, currently an engineer must always keep in mind the process that is to be used to construct the object. This limits the creativity of the engineer. In fact, the engineer is never quite sure whether the object can be built since, at present, almost no formal methods exist to determine the feasibility of manufacturing an object for most processes. To alleviate this problem, practical algorithms are needed to determine, given an arbitrary object, whether or not it can be built using any of the known manufacturing processes. The benefits of such an "intelligent" CAD/CAM system would be two-fold. First, an engineer would have an algorithm with which to verify whether an object can be created using the manufacturing process intended (i.e. a type of automatic design-verification). Second, a list of the possible manufacturing processes that can build a particular object would allow the engineer to design a product and then determine which manufacturing process would be most cost effective. Recently, there has been a flurry of activity, among computational geometers, concerned with the study of manufacturing processes from this Computer Aided Manufacturing perspective.

Below you will find papers that deal with geometric aspects of several manufacturing processes.

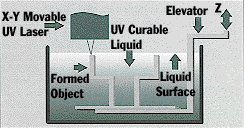
Stereolithography:

Stereolithography is a process for building an object layer by layer by scanning a laser beam on the surface of a plastic that solidifies at the point of contact with the laser. You may want to read about the basics of stereolithography before diving into the geometry in the paper below.

Gravity Casting:

Gravity casting is a manufacturing method that uses gravity to do some of the work. A molten metal (or other fluid) is poured into a cast or mold through a hole called the pingate. After the fluid hardens to mold is opened to release the object. The first paper below deals with gravity casting of polygons in 2 dimensions. The second paper deals with polyhedra in 3 dimensions.

Pingate Location in Injection Molding:

In injection molding the molten plastic is injected via the pingate into the mold under pressure. The plastic hardens quickly and must reach all parts of the mold before it hardens. An important problem here is the location of the pingate. For example, one may want to minimize the maximum distance that the molten plastic must travel to reach every corner of the object. One may also wish to minimize the number of bends in the trajectory that the fluid must travel. Such bends cause turbulence in the flow of the fluid which in turn causes imperfections in the finished product. In the paper below several agorithms are given for computing optimal locations of the pingate in flat (polygonal) objects.

Research Interests Homepage