
The reading machine considered here was developped in the mid-sixties with two goals in mind: Cost (hence simplicity) and Efficiency (able to recognize a wide range of fonts). The overall structure of the machine consists of:
This intelligent machine starts with an empty lookup table - an empty brain. But after a short training session, the machine - simple minded as it is - was claimed to have a success ratio of 99.9%
Obviously the heart (or the brain?) of the machine is its Feature Extraction algorithm, which was developped by J.K.Clemens for his Ph.D. thesis [1]. It is this elegant algorithm that we will describe below. Note that it is presented here only for its academic interest as an early character recognition algorithm that uses hysteresis smoothing. Today, every desktop scanner comes with a powerful document analysis software that uses more efficient algorithms. Note also that I couldn't find Clemens' paper nor any other information on the machine: as a first consequence, everything I shall say here has been said in class by professor Toussaint. As a second consequence, I don't know what happened to that wonder machine...
BY THE WAY if anybody has any information on this machine, I would be interested to know about it...
[1] Clemens,J.K., "Optical character recognition for reading machine applications", Ph.D. thesis, Dept. Elec. Eng., M.I.T., August 1965

As an input the algorithm receives the bitmap representation of the character to identify, as illustrated above. Since we want the feature vectors to be invariant under scaling (and obviously, under translation), the very first information to extract from the isolated character concerns its X and Y dimensions: this can be done by using a simple contour-tracing algorithm (see below, left) but then we might not obtain the true dimensions of the character (imagine contour-tracing the character ' i ', and missing the dot).
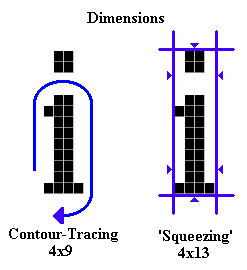
Although obtaining the real dimensions might not be essential to the algorithm, we will assume here that it is. Our implementation computes the true dimensions by squeezing the character between vertical lines to the left and right, and horizontal lines above and below (as above, right). But even then, we still need a contour tracing algorithm...
This is a one-pass algorithm: the feature vectors are extracted as we contour-trace the character. Contour tracing is not the main topic of this presentation, and we assume the reader is familiar with either the square-tracing or the Moore-tracing algorithm (we use the latter in our implementation). To know more about contour-tracing, refer to this paper (postscript file).
The main (and brilliant) idea of the algorithm is that the crawling bug (i.e. the pixel we are visiting while contour-tracing) drags with it a frame, the Hysteresis Window. The initial position of the Window with respect to the bug is as shown below (i). Since it is in contact with both the upper and right parts of the frame, the bug will drag the Window with it if it starts moving upward or rightward (ii). If it then changes its direction to go downward or to the left, the frame will remain in place until the bug comes in contact with the other side of the Window (iii). At that precise moment, that is WHENEVER THE BUG SWITCHES FROM UPPER TO LOWER OR FROM LEFT TO RIGHT SIDES OF THE WINDOW (and equivalently, from lower to upper / right to left), A FEATURE IS RECORDED. The figure below illustrates the whole process for our sample character. See also the next figure.
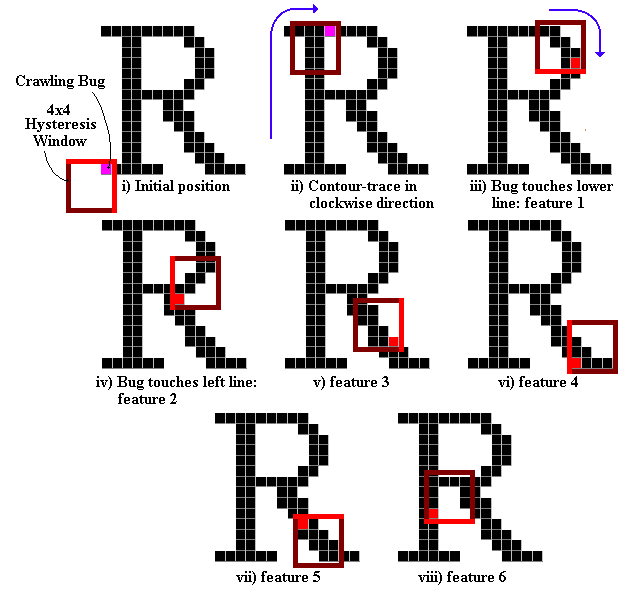
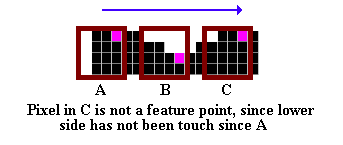 The features recorded
will obviously depend on the size of the Hysteresis Window: a Window greater
than the character itself will find no features, and a 2x2 Window will
typically find more features than a larger Window. Clemens suggests that
the x and y dimensions of the Hysteresis Window be respectively set to
1/4 of the X and Y dimensions of the character. Empirically, these dimensions
correspond to the average sizes of the serifs and hence should be optimal
to record only relevant features. This is a good example of Hysteresis
smoothing in 2-dimensions to get rid of noise (serifs). (and it would
sure have been fun to demonstrate it with an applet!)
The features recorded
will obviously depend on the size of the Hysteresis Window: a Window greater
than the character itself will find no features, and a 2x2 Window will
typically find more features than a larger Window. Clemens suggests that
the x and y dimensions of the Hysteresis Window be respectively set to
1/4 of the X and Y dimensions of the character. Empirically, these dimensions
correspond to the average sizes of the serifs and hence should be optimal
to record only relevant features. This is a good example of Hysteresis
smoothing in 2-dimensions to get rid of noise (serifs). (and it would
sure have been fun to demonstrate it with an applet!)
The features are recorded in a code-word. As illustrated below, only the minimal information - the sequence of side switches - needs to be remembered. But this information might not be enough to characterize a pattern: Consider for example the characters ' i ' and ' l ' - both have the same code-word and would thus be mistaken. This is why the coordinate-word is introduced, where the quadrant in which the feature was detected is recorded.
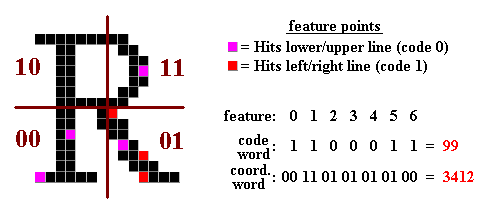
So we get FEATURE VECTOR = (Code-Word, Coordinate-Word)
A few notes on the algorithm: first, it should be observed that the feature vectors are invariant under translation and scaling, but not under rotation and shearing. It should thus be assumed that the input bitmap represents one perfectly levelled character. The feature vectors might vary from one font to another, so the machine might need to be trained on all the potential fonts it will have to recognize. One should also note that the algorithm is designed to extract features from both upper and lower-case letters from the english alphabet (that is français à éviter). It could as easily characterize numerals, but punctuation might be a problem (e.g. will it differentiate ' . ' and ' , ').
Here is a sample output on the R character we used in this presentation:
XXXXXXXXX XX XX XX XX XX XX XX XX XX XX XXXXXXX XX XX XX XXX XX XX XX XX XX XXX XX XXX XXXXXX XXXX SIZE OF BITMAP: 21 x 28 SIZE OF CHARACTER: 14 x 14 Hit BOTTOM at (3,10) Hit LEFT at (7,7) Hit RIGHT at (11,10) Hit LEFT at (13,10) Hit TOP at (10,8) Hit BOTTOM at (9,3) 6 Feature points Code-Word: 1 1 0 0 0 1 1 = 99 Coordinate-Word: 00 11 01 01 01 01 00 = 3412