McGill University:
School of Computer Science
Winter 1997 Class Notes for 308-251B

DATA STRUCTURES AND ALGORITHMS

Topic #11: Game trees. Alpha-beta search

Game Tree

We will set up a framework for playing a two-person game in which the two players alternate making moves.

The game can normally be represented as a tree where the nodes represent the current status of the game and the edges represent the moves. The game tree consists of all possible moves for the current players starting at the root and all possible moves for the next player as the children of these nodes, and so forth, as far into the future of the game as desired. The leaves of the game tree represent terminal positions as one where the outcome of the game is clear (a win, a loss, a draw, a payoff). Each terminal position has a score. High scores are good. For example, we may associate 1 with a win, 0 with a draw and -1 with a loss.

Example : Game of NIM

In this game, several piles of sticks are given. We represent the configuration of the piles by a monotone sequence of integers, such as (1,3,5,7) or (2,2,3,9,110). A player may remove, in one turn, any number of sticks from one pile of his/her choice. Thus, (1,3,5,7) would become (1,1,3,5) if the player were to remove 6 sticks from the last pile. The player who takes the last stick loses. The NIM game (1, 2, 2) can be presented by Fig. 1. where 1 is a win and 0 is a loss.

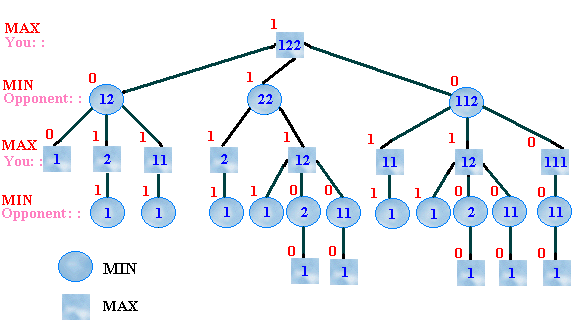
Figure 1: Game Tree for (1, 2, 2) NIM


In Figure 1 , the number in the root shows that in the beginning there are five sticks which consists of three sets, 1, 2, 2. Suppose you are the player who makes the first move. You may take one or two sticks. After your move, it is your opponent's turn and the numbers in the nodes represent the sticks left. Then the opponent moves one or two sticks and the status is shown in the next nodes and so on until there is one stick left.

Now, we can use this game tree to analyze the best possible move. For each player, the best move is to make the opponent lose and make himself/herself win. So, one should make the move to get the MAX score and force their opponent to get the MIN score. A loss is represented by "0" and a win is presented by "1". The MAX nodes represent the position of the current player and the MIN nodes represent the position of the opponent. Since the goal of this game is that the player who removes the last stick loses, the scores are assigned to "0" if the leaves are at MAX nodes and the scores are assigned to "1" if the leaves are MIN. Then we back up the scores to assign the internal nodes from the bottom nodes. At MAX nodes, choose the MAXIMUM score among the children; at MIN nodes, choose the MINIMUM score of the children as the lower the score the better for MIN. So MIN is will try to minimize the score in order to win while MAX will try to maximize it. In this manner, we may compute the scores of the internal nodes from the bottom up. In the example of figure 1, the root node is "1", and thus corresponds to a win for the first player. The first player should pick a child position that corresponds to a "1".

MiniMax Game Tree

In a MiniMax tree, one can view in its entire form, the score values at each of the levels of the tree at any given point during the game. By viewing this tree, a player may be able to forsee which moves are more advantageous and beneficial for themselves. The root of the tree represents the position of the current player, thus, depending on the number of levels that is to be searched, all odd levels represent the first player while the even levels represent the second player.

In a two player game, the first player moves with MAX score and the second player moves with MIN score. A minimax search is used to determine all possible continuations of the game up to a desired level. A score is originally assigned to the leaf, (usuall we do that when we reach a leaf), then by evaluating each possible set of moves, a score is assigned to the upper level by the minimax algorithm. The minimax algorithm performs a preorder traversal and computes the scores on the fly. The same would be obtained by a simple recursive algorithm. The rule is as follows:

 minmax(u)
    {   //u is the node you want to score

            if u is a leaf return score of u;
            else if  u in a min node
                for all childern of u: v1, .. vn ;
                        return min{ minmaxv1),..., minmax(vn)}
            else for all childern of u: v1, .. vn ;
                        return max{ minmax(v1),..., minmax(vn)}
        }
 


Note: If we know the scores of all the nodes, it would be futile and boring to play the game because we would know the outcomes already (against a clever opponent). The scores are the same as the outcome of a game that would result in two infinitely clever players would play each other starting from that position.

The complexity of the algorithm is equal to the number of nodes in the tree.

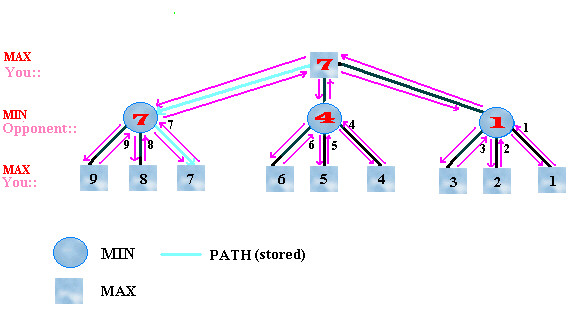
Figure 2: Minimax Search


Figure 2 shows how the minimax algorithm works. There is a game tree which consists of all possible moves. The root represents the current player and the children of the root represents the opponent. And the leaves contain the scores and from there we assign score to the internal nodes by the minmax algorithm. We want to find the best move for the current player. So at the position of the current player, we choose the MAX score of its children; and at the position of opponent, we choose the MIN score of its children. Before the game starts the score for MIN Nodes is set to +infinity and decreases with time. For MAX nodes, scores starts with -infinity and increases with time.

Bounded Lookahead in Large Tree

In large trees, it is quite impossible to search all the nodes. The next best thing is to trim the tree to a few levels and pretend that it is a good approximation of the (unknown) minimax tree by assigning scores to its leaves. The difference now is that the scores are no longer exact, but only educated guesses. The scores obtained in this manner are said to be calculated with the aid of an evaluation function. Evaluation functions are constructed by the user based upon insight and experience. We may still employ the minimax algorithm to go the required levels deep in the recursion tree of moves, compute the scores at the leaves and then propogate the score up the tree using the minmas algorithm:
evalutemin (u)     {//u in a min node
                    if u is a leaf then
                                        return the evaluated score of this leaf
                      else
                                let v1,v2,v3, vn be the childern of U;
                                return min { evalutemax(v1),....,evalutemax(Vn)}
                           }
 
evalutemax (u)     {//u in a mx node
                    if u is a leaf then
                                        return the evaluated score of this leaf
                      else
                                let v1,v2,v3, vn be the childern of U;
                                return max { evalutemin(v1),....,evualutemin(Vn)}
 
                           }
 
 
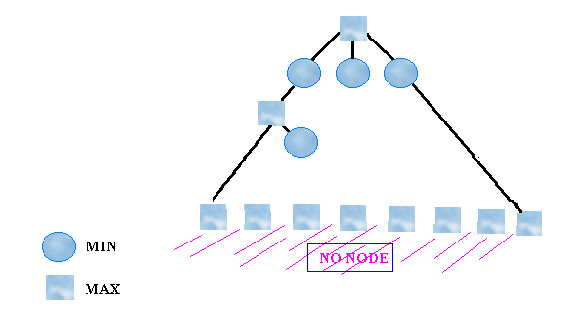Figure 3: Large tree


Alpha-Beta Search

ALPHA-BETA search is a method that reduces the number of nodes explored in Minimax strategy. It reduces the time required for the search and it must be restricted so that no time is to be wasted searching moves that are obviously bad for the current player. The exact implementation of alpha-beta keeps track of the best move for each side as it moves throughout the tree.

We proceed in the same (preorder) way as for the minimax algorithm. For the MIN nodes, the score computed starts with +infinity and decreases with time. For MAX nodes, scores computed starts with -infinity and increase with time.

The efficiency of the Alpha-Beta procedure depends on the order in which successors of a node are examined. If we were lucky, at a MIN node we would always consider the nodes in order from low to high score and at a MAX node the nodes in order from high to low score. In general it can be shown that in the most favorable circumstances the alpha-beta search opens as many leaves as minimax on a game tree with double its depth.

Here is an example of Alpha-Beta search:

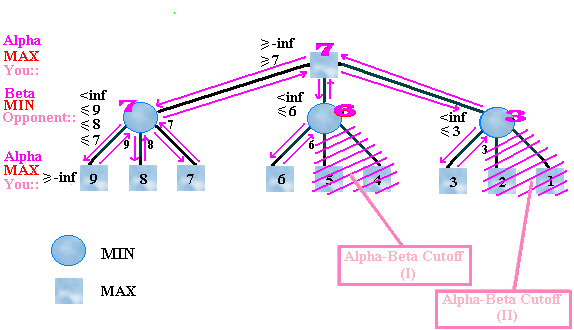
Figure 4: Alpha-beta search

At the MAX node we look at the score of its children to make the best move. Initially the scores are not assigned so we have to go down the tree to the leaves compute their score and then carry the scores up the tree. Here the MAX chooses the move with score 7 because in this case the worst MIN can do is to minimize MAX's score to 7. If MAX makes the move represented by the second child, MIN can minimize the score to 6 which is less than the least score among the children of the first child of MAX (noting that MIN will always try to minimize the score). Hence MAX will not look any further in this subtree for this move is clearly worse than the first one. Same is the case of the third child of MAX.


Alpha-Beta algorithm:

(Corrected by Long Cheong, 2012.7.20)

An alpha-beta algorithm consists of two functions: evalutemin and evalutemax. If calling from a MIN nodes, function evalutemin is used, while calling from a MAX node, function evalutemax is used.
We begin with the MAX player by calling evaluatemax(u, +infinity) where u is the starting position of the game.

   evalutemin(u,  B) //u is a min node

                    Alpha=+infinity;
                             {
 
                                    {
                             Return Alpha;
    {
                    if u =leaf return the score;
                    else
                             for all children v of u
                                    Val = evalutemax(v,  B);
                                    alpha= Min{alpha, Val};
                                    if  Alpha<=beta  then exit loop;
                              }
                    Return alpha;
}
    evalutemax(u,B)   // u is a Max node
    {
                            alpha=-infinity;
                             if u=leaf return the score;
                             else
                                    for all children v of u
                                        Val = evalutemin(v, B);
                                        Alpha = Max{Alpha, Val};
                                        if Alpha >= Beta then exit loop;
                                    }
      }

Java Applet

The following is a simple Java Applet Demo to demonstrate the Minimax search shown in Fig. 2 .

The source.


.

Links
Animation of a Minimax Algorithm in Zeus
by Sam Weber, Digital Equipment Corporation's System Research Center
Java Games
EarthWeb Incorporated

References

Web page creators

This web page was created by
Last updated August 9, 1999 Haroon Ali Agha
Copyright © 1997, Pui Yee Chan, Hiu Yin Choi, Zhifeng Xiao. All rights reserved. Reproduction of all or part of this work is permitted for educational or research use provided that this copyright notice is included in any copy. Disclaimer: this collection of notes is experimental, and does not serve as-is as a substitute for attendance in the actual class.